تبرزین (هندسه)

تبرزین (به انگلیسی: tomahawk) ابزاری در هندسه است که از آن برای تقسیم کردن یک زاویه به سه قسمت مساوی (تثلیث زاویه) استفاده میکنند. شکل ظاهری آن، شامل یک نیمدایره و دو پارهخط است که بهصورتی قرار دارند که شکل یک تبرزین را تداعی میکند که یک نوع تبر آمریکایی است. ابزاری مشابه نیز وجد داشته که به آن چاقوی کفاش گفته میشده، ولی امروزه این نام بیشتر به شکل هندسی دیگری به نام Arbelos اطلاق میشود. (یک مثلث با اضلاع منحنی که توسط سه نیم دایرهٔ مماس برهم، تشکیل میشود)
توضیحات
[ویرایش]شکل اصلی تبرزین، شامل این اجزاء میشود: یک نیمدایره (تیغهٔ تبر)، یک پارهخط به اندازهٔ شعاع نیمدایره که در راستای قطر آن ادامه داده شدهاست (نوک یا سوزن تبر) و یک پارهخط به اندازهٔ دلخواه (به عنوان دستهٔ تبر) عمود بر قطر نیمدایره. برای ساختن این ابزار به صورت فیزیکی، ممکن است دسته و نوک (سوزن) آن، ضخیمتر در نظر گرفته شود، به اندازهای که پارهخط موازی با دستهٔ تبر، همچنان بخشی از محدودهٔ شکل هندسی باشد. برخلاف روش تثلیث زاویه با گونیا، طرف دیگر دسته (که ضخیمتر میشود) لازم نیست که موازی با پارهخط آن ساخته شود.
در برخی منابع به جای نیمدایره از دایرهٔ کامل استفاده میشود، یا تبرزین از قسمت نیمدایره هم موازی با قطر آن نیز ضخیم میشود، اما این تغییرات تفاوتی در عملکرد تبرزین به عنوان یک ابزار تثلیث زاویه ایجاد نمیکند.
تثلیث زاویه
[ویرایش]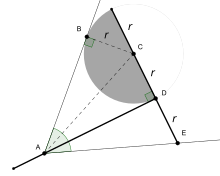
برای تثلیث زاویه با تبرزین، آن را بهصورتی قرار میدهیم که دستهٔ آن از رأس زاویه بگذرد، همینطور یکی از اضلاع زاویه باید با نیمدایرهٔ تبرزین مماس شود و همچنین سوزن آن با ضلع دیگر زاویه برخورد کند. یکی از خطوطی که زاویه را به سه قسمت مساوی تقسیم میکند، پارهخط دستهٔ تبر است و خط دیگر، از مرکز نیمدایره میگذرد. اگر زاویهای بسیار حاده (تند) باشد، با توجه به طول دستهٔ تبرزین، ممکن است نتوان تبرزین را داخل زاویه قرار داد. اما این مشکل را میتوان با این راهکار برطرف کرد؛ زاویه را (اضلاع آن را) تا زمانی که تبرزین داخل آن قرار بگیرد، دو برابر میکنیم، حال پس از انجام تثلیث زاویه، آن را نصف کنیم تا (اضلاع آن) به اندازهٔ اولیه بازگردد.
اگر رأس زاویه را A، نقطهٔ مماس نیمدایره را B، مرکز نیمدایره را C، ابتدای دستهٔ تبر را D، و سوزن تبر را E بنامیم، آنگاه مثلثهای ACD و ADE هر دو مثلثهای قائمالزاویهای هستند که دارای قاعده و ارتفاع یکسان هستند، پس با یکدیگر متشابه هستند. به علت این که ضلعهای AB و BC هرکدام به ترتیب مماس بر نیمدایره و شعاع نیمدایره در نظر گرفته شدهاند، بنابراین تشکیل زاویهٔ قائمه میدهند، بنابراین مثلث ABC نیز قائمالزاویه است. همچنین این مثلث، وتری مشترک با مثلث ACD دارد و همچنین BC = CD، بنابراین این مثلث نیز با دو مثلث دیگر متشابه است که بیانگر این است که سه زاویهای که در رأس زاویهٔ اصلی ایجاد شدهاست، با یکدیگر برابر هستند.
اگر چه تبرزین ممکن است خودش به وسیلهٔ خطکش و پرگار ساخته شده باشد و ممکن است برای تثلیث زاویه مورد استفاده قرار بگیرد، اما تئوری سال ۱۸۳۷ Pierre Wantzel را که بیان میکند زاویههای دلخواه نمیتوانند به وسیلهٔ خطکش نشانهگذاری نشده و پرگار به سه قسمت تقسیم شوند را نقض نمیکند، به این دلیل که قرار دادن تبرزین ساخته شده در منطقهٔ خواسته شده یک نوعی از neusis است نمیتوان از آن در روشهای خطکش و پرگار استفاده کرد.
تاریخچه
[ویرایش]مخترع تبرزین ناشناخته است اما اولین مراجع مربوط به آن از فرانسهٔ قرن ۱۹ میآید. تاریخهای آن حداقل به ۱۸۳۵ برمیگردد، زمانی که آن در کتابی توسط Claude Lucien Bergery به نام Géométrie appliquée à l'industrie, à l'usage des artistes et des ouvriers (3rd edition) منتشر شد. اثر دیگری از این نوع تقسیمبندی توسط Henri Brocard در سال ۱۸۷۷ منتشر شد. Brocard ویژگیهای ابداع خودش را مربوط به یک یادداشت در سال ۱۸۶۳ توسط یک مأمور نیروی دریایی فرانسه به نام Pierre-Joseph Glotin دانست.
منایع
[ویرایش]- مشارکتکنندگان ویکیپدیا. «Tomahawk (geometry)». در دانشنامهٔ ویکیپدیای انگلیسی، بازبینیشده در ۱۱ ژانویه ۲۰۱۷.
